前言
普通的素数筛暴力的二重循环的算法时间复杂度是O(n^2),用sqrt的话可以优化一下,算法时间复杂度可以提升一下,但是有时候遇到1e7的还是无法满足,时间就会超时。
埃氏筛的算法时间复杂度是O(nloglogn)。
欧拉筛的算法时间复杂度是O(n)。
暴力筛法
#include<iostream>
#include<cmath>
using namespace std;
int isprime(int n){ 判断素数
int i;
for(i=2;i<=n;i++)
{
if(i%n==0)
{
return 0; 不是素数
}
}
return 1;是素数
}
void prime(int n){ 寻找素数
int i,j;
for(int i=2;i<=n;i++)
{
for(int j=2;j < i;j++)
{
if(i%j==0)
{
break;
}
}
cout << i << " ";
}
}
int main()
{
return 0;
}用sqrt优化后的
#include<iostream>
#include<cmath>
using namespace std;
int isprime(int n){ 判断素数
int i;
for(i=2;i<=sqrt(n);i++)
{
if(i%n==0)
{
return 0; 不是素数
}
}
return 1;是素数
}
int main()
{
return 0;
}埃氏筛
原理:首先将2到n范围内的整数记录下来。其中2是最小的素数,将表中所有2的倍数划去,表中剩下的最小数字就是3,它不能被更小的数整除了,所以3个素数,然后再将表中所有3的倍数都划去…..以此类推(如果表中剩余的最小数是m,那么m就是素数,然后将表中所有m的倍数都划去),反复操作,就能依次枚举n以内的素数。
例如:求1~20之内的素数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
第一趟:从2开始,将2的倍数划去,
2 3 5 7 9 11 13 15 17 19
第二趟:从3开始,将3的倍数划去
2 3 5 7 11 13 17 19
……..
后面的只要是素数的就不会进行操作,直接跳过,一开始时初始化默认全是素数。
#include<iostream>
#include<cmath>
using namespace std;
int visit[maxn];
void Prime()
{
for(int i=0;i < maxn;i++) 进行初始化,都是素数,值=0是素数,值=1不是素数
{
visit[i]=0;
}
visit[0]=visit[1]=1; 0和1不是素数
for(int i=2;i<=maxn;i++)
{
if(!visit[i])//如果是素数
{
for(int j=i*i;j <= maxn;j+=i) 进行循环把后面的倍数都划去
{
visit[j]=1;
}
}
}
}
int main()
{
return 0;
}欧拉筛
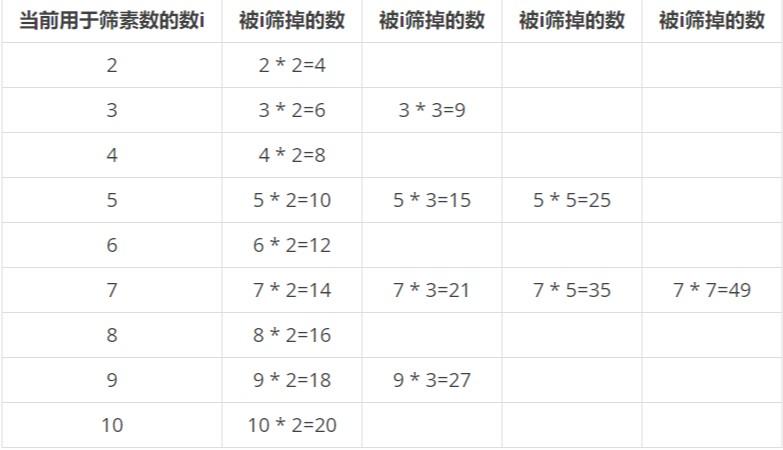
原理:在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的
#include<iostream>
#include<cmath>
using namespace std;
int prime[maxn]; prime[0]可以用来计数,也可以额外定义一个来计数
int visit[maxn];
void Prime(){
for(int i=0;i < maxn;i++) 进行初始化,都是素数,值=0是素数,值=1不是素数
{
visit[i]=0;
prime[i]=0;
}
for(int i=2;i<=maxn;i++)
{
if(!visit[i]) 记录素数
{
prime[++prime[0]]=i; 同时存找到的素数
}
for(int j=1;j<=prime[0]&&i*prime[j]<=maxn;j++)
{
visit[i*prime[j]]=1;
if(i%prime[j]==0)
{
break;
}
}
}
}
int main()
{
return 0;
}