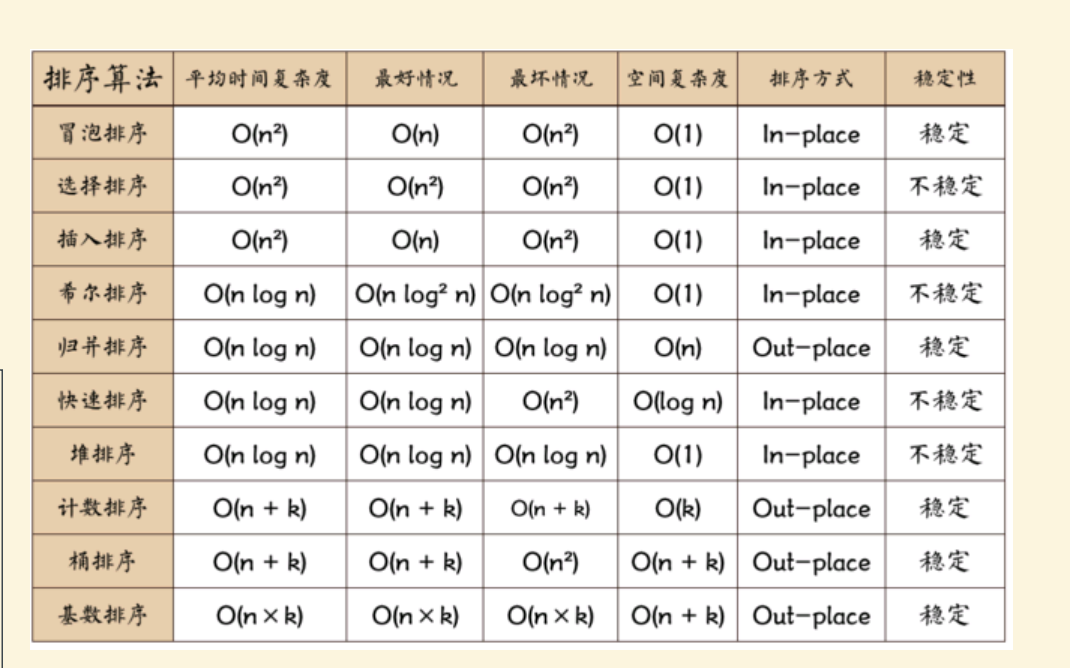
时间复杂度和空间复杂度
下图就是本篇文章说到的排序算法,之后可能会补充其它的排序算法吧~
冒泡排序(蛮力法)
过程如下
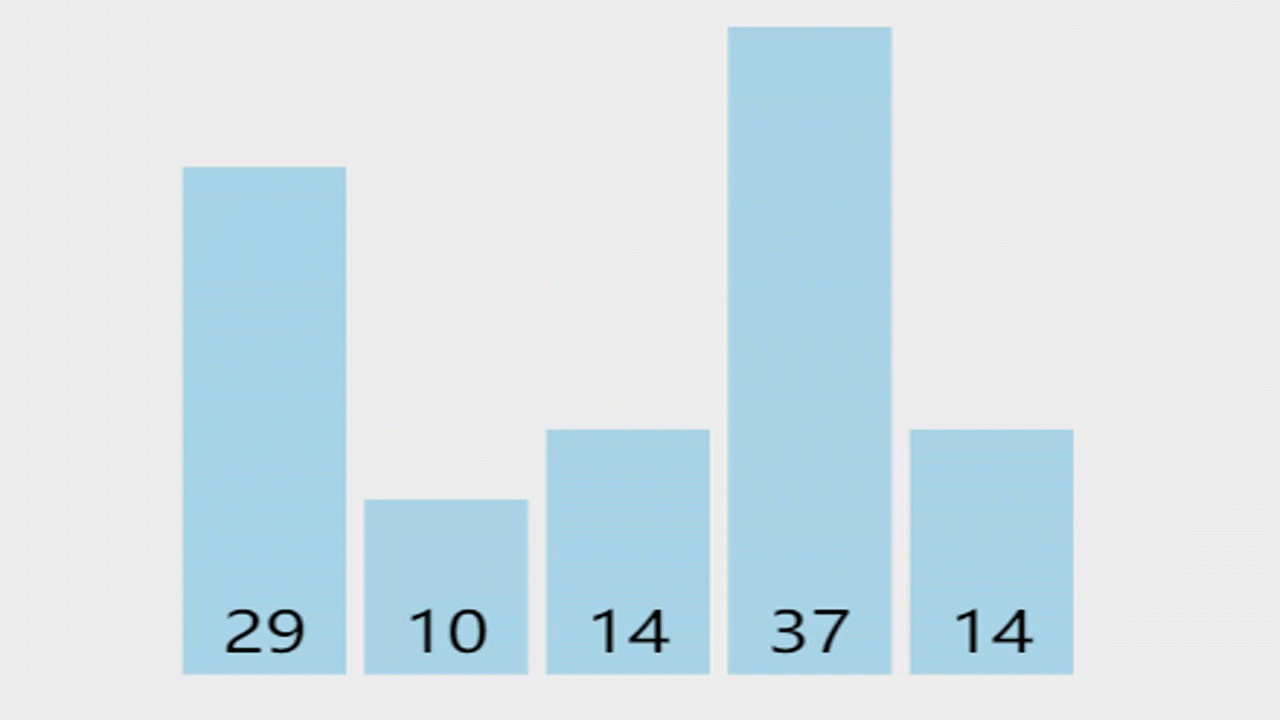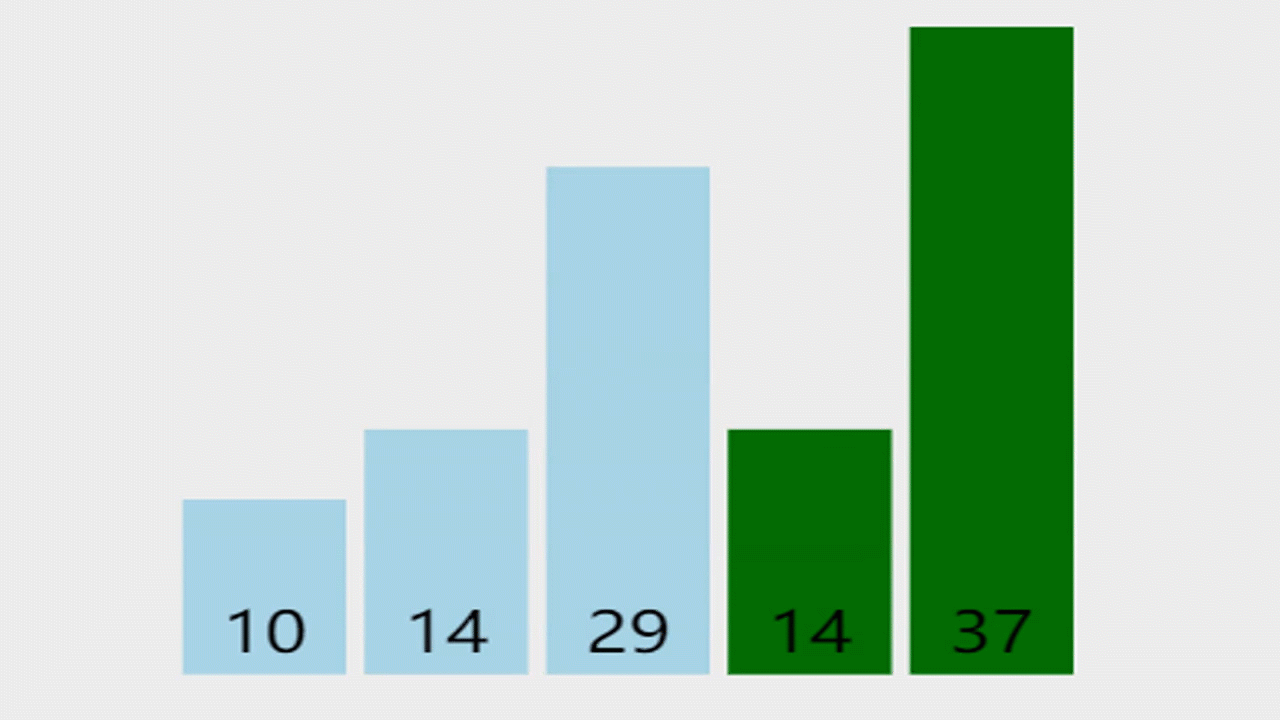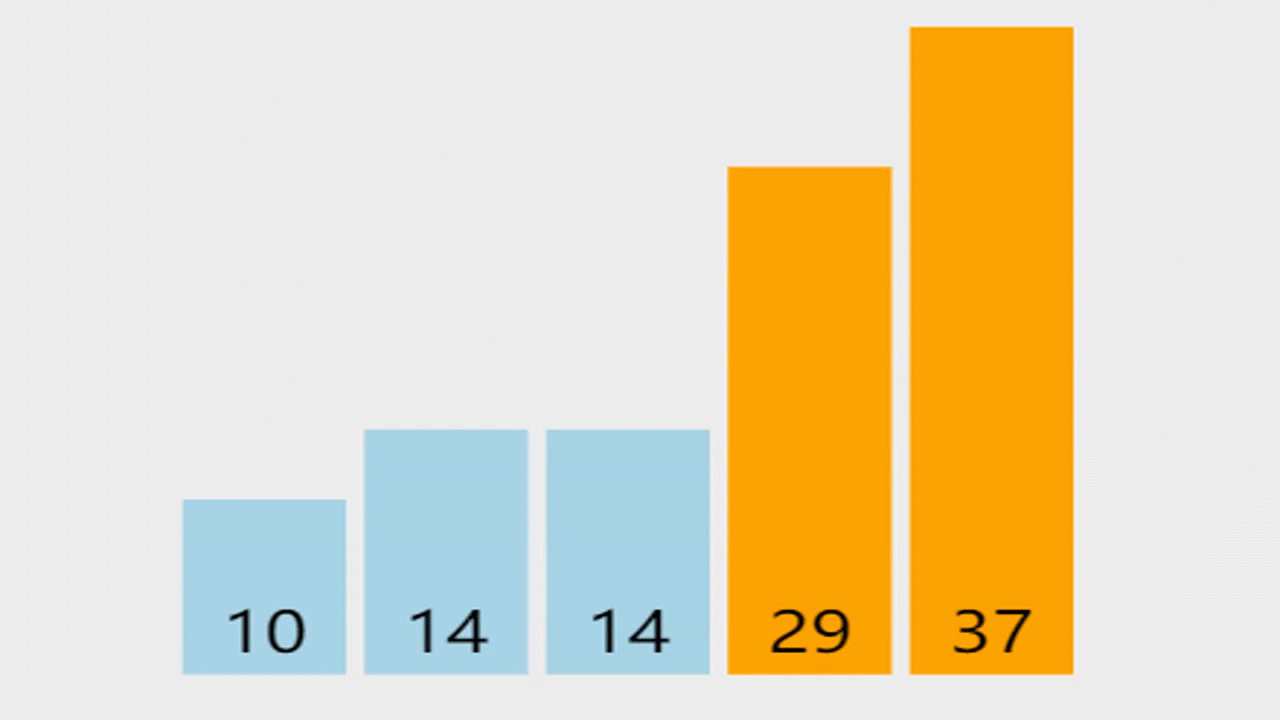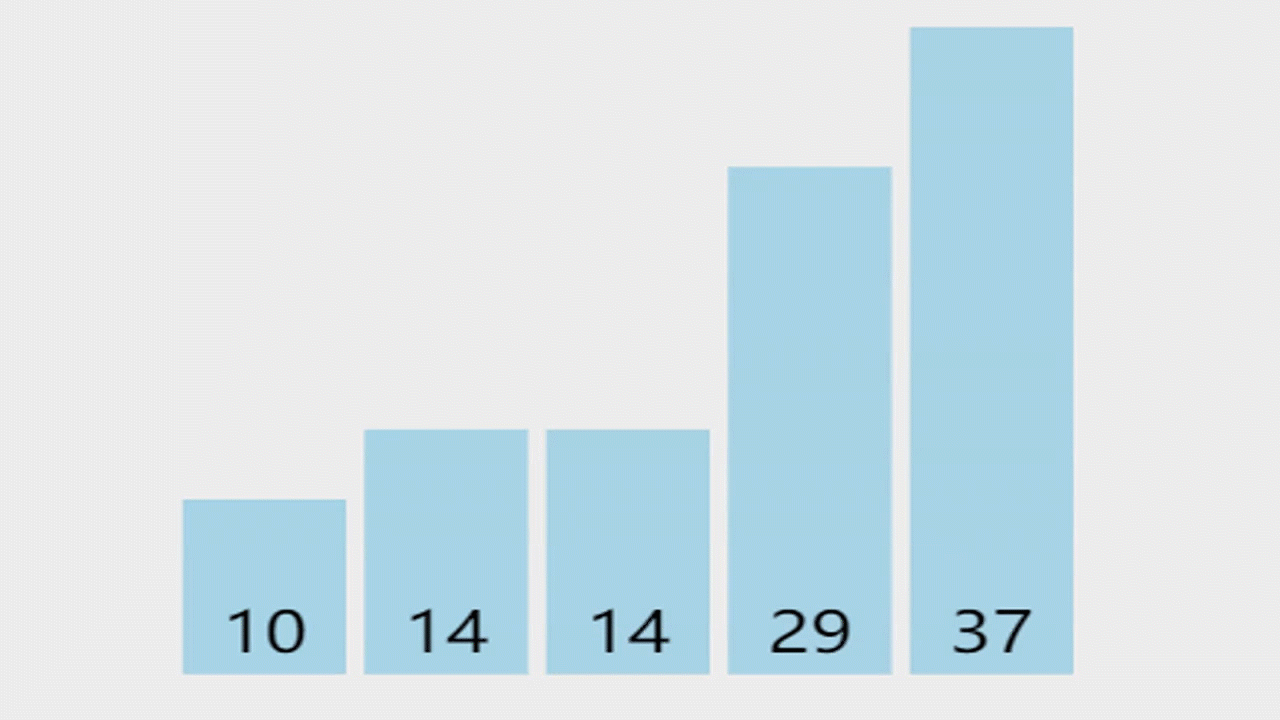
这里就以简单的以升序为例,因为冒泡排序的思想都是一样的,所以我就不做过多的阐述。
思想:对无序区从前向后依次比较相邻记录,若反序则交换,从而使得值较小的记录向前移,值较大的记录向后移(都说冒泡了,就跟在水中的气泡一样,体积大的先浮上来)
代码如下:
void bubble_sort(int arr[], int len)
{
int i, j , temp;
for (i = 0; i < len - 1; i++)
{
for (j = 0; j < len - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}优化操作
void bubble_sort(int arr[], int len)
{
int i, j , temp;
bool flag=true;
for (i = 0; i < len - 1; i++)
{
for (j = 0; j < len - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag=false;
}
}
if(flag)break;
}
}选择排序(蛮力法)
过程如下
思想:在无序区找出最小的记录,然后将它与无序区的第一个记录交换,使得有序去扩展一个记录,同时无序区减少一个记录。
代码如下:
void selection_sort(int arr[], int len)
{
int i,j,index,temp;
for(i=0;i < len;i++)
{
index=i;
for(j=i+1;j < len;j++)
{
if(arr[j] < arr[index])index=j;
}
if(index != i)
{
temp=arr[i];
arr[i]=arr[index];
arr[index]=temp;
}
}
}插入排序(减治法)
过程如下
思想:插入排序(insertion sort)属于减治法的减一技术,即每一趟排序后将问题规模减少1,其基本思想的是依次将待排序序列中的每一个记录插入到一个已经排好序列的序列中,直到全部记录都排好序。
代码如下:
void Insertion_Sort(int arr[], int len)
{
int i,j;
for(i=2;i <= len;i++)
{
arr[0]=arr[i];
for(j=i-1;arr[0] < arr[j];j--)
{
arr[j+1]=arr[j];
}
arr[j+1]=arr[0];
}
}希尔排序(分治法)
过程如下
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”,是直接插入排序算法的一种更高效的改进版本。希尔排序是非常稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
思想:
原文:The method starts by sorting pairs of elements far apart from each other, then progressively reducing the gap between elements to be compared. Starting with far apart elements, it can move some out-of-place elements into position faster than a simple nearest neighbor exchange.
这里就长话短说吧,如果你有更好的思想,可以邮箱联系–>希尔排序其实就将待排序列分成很多个组,但是分组呢不是随便分的,是按照差距(gap)分组,差距(gap)怎么计算呢,就是假如你有15个数,n=15,然后差距(gap)=n/2=7。
例如图中的
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 数组 | 4 | 2 | 6 | 3 | 8 | 1 | 2 | 3 | 4 | 6 | 2 | 9 | 3 | 6 | 8 |
| 组别 | 下标内部进行比较 |
| 第一组 | 0 , 7 |
| 第二组 | 1 , 8 |
| 第三组 | 2 , 9 |
| 第四组 | 3 , 10 |
| 第五组 | 4 , 11 |
| 第六组 | 5 , 12 |
| 第七组 | 6 , 13 |
| 第八组 | 0 , 7 , 14 |
然后就进行比较,例如:第一组,下标为0和7的值进行比较,4 > 3,则交换,一直按顺序来做。做完一轮后,继续缩小增量,此时的gap=7/2=3
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 数组 | 3 | 2 | 6 | 2 | 8 | 1 | 2 | 4 | 4 | 6 | 3 | 9 | 3 | 6 | 8 |
| 组别 | 下标内部进行比较 |
| 第一组 | 0 , 3 , 6 , 9 , 12 |
| 第二组 | 1 , 4 , 7 , 10 , 13 |
| 第三组 | 2 , 5 , 8 , 11 , 14 |
以此类推(貌似过程是这样子,如果有错的话,请及时发送给我的邮箱,非常感谢你~)…
代码如下(下标从0开始,如果是从1开始的话,要修改代码):
void Shell_Sort(int arr[], int len)
{
int gap,j;
for(gap=len/2;gap > 0;gap/=2)
{
for(int i=gap;i < len;i++)
{
int temp=arr[i];
for(j=i;j >= gap&&temp < arr[j-gap];j-=gap)
{
arr[j]=arr[j-gap];
}
arr[j]=temp;
}
}
}归并排序(分治法)
过程如下
思想:归并排序首先执行划分过程,将序列划分为两个序列,如果序列为1则划分结束,否则继续划分,然后将已有序的子序列合并,得到完全有序的序列。
代码如下:
平常的模版
void Merge(int r[ ], int r1[ ], int s, int m, int t)
{
int i = s, j = m + 1, k = s;
while (i <= m && j <= t)
{
if (r[i] <= r[j]) r1[k++] = r[i++];
else r1[k++] = r[j++];
}
while (i <= m) r1[k++] = r[i++];
while (j <= t) r1[k++] = r[j++];
}
void MergeSort(int r[ ], int s, int t)
{
int m;
int r1[1000] = {0};
if (s == t) return;
else
{
m = (s + t)/2;
MergeSort(r, s, m);
MergeSort(r, m+1, t);
Merge(r, r1, s, m, t);
for (int i = s; i <= t; i++)r[i] = r1[i];
}
}对比下面y总的其实都是差不多,都是要两个数组实现,只不过把两个代码合并了。
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int tmp[r-l+1];
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else tmp[k ++ ] = q[j ++ ];
while (i <= mid) tmp[k ++ ] = q[i ++ ];
while (j <= r) tmp[k ++ ] = q[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}快速排序(分治法)
过程如下:
思想:先从数列中取出一个数作为基准数。分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。再对左右区间重复第二步,直到各区间只有一个数。
代码如下:
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
while (q[ ++ i] < x);
while (q[-- j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}堆排序(分治法)
堆的定义:
堆:完全二叉树 + 满足某种条件。父亲结点比左右儿子小(小根堆)或 父亲结点比左右儿子大(大根堆),一般升序用大根堆,降序用小根堆,自己画,自己想象。
堆(heap)有时被称为优先队列(priority queue)。堆和队列有相似地方,在堆底插入元素,在堆顶取出元素,但是堆中元素的排列不是按照到来的先后顺序,而是按照一定的优先顺序排列的
堆排序思想:
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
如果不太了解堆排序的可以看这篇文章,这篇是我看对比了这么多博客之后,还是不错的。
过程如下:
模板代码如下(来自y总):
h[N]存储堆中的值, h[1]是堆顶,x的左儿子是2x, 右儿子是2x + 1
ph[k]存储第k个插入的点在堆中的位置
hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;
交换两个点,及其映射关系
void heap_swap(int a, int b)
{
swap(ph[hp[a]],ph[hp[b]]);
swap(hp[a], hp[b]);
swap(h[a], h[b]);
}
void down(int u)
{
int t = u;
if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t)
{
heap_swap(u, t);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u] < h[u / 2])
{
heap_swap(u, u / 2);
u >>= 1;
}
}
O(n)建堆
for (int i = n / 2; i; i -- ) down(i);总的来说,就是要先建个初始堆,然后就进行堆排序
计数排序
过程如下:
貌似只能0~9,其他情况需要具体分析,这里就不写代码了.
码字中ing…莫得办法,高质量的博客的就得时间