最小生成树

概念
prim算法（点）
(kruskal)克鲁斯卡尔算法（边）

概念

在无向图中，连通而且不含有圈（环路）的图称为树。所以下面的两种算法中的重要问题是判断圈，即每次的新加入一个点或者边的同时又要判断是否形成圈。Prim算法适用于稠密图，Kruskal适用于稀疏图。

接来下将一下prim算法和kruskal算法，这两种算法都基于贪心法，因为最小生成树（Minimal Spanning Tree，MST）问题满足贪心法的 “最优性原理” ，即全局最优包含局部最优。

prim算法（点）

思想：对点进行贪心操作。从任意一个点 u 开始，把距离它最近的点 v 加入到 T 中；下一步，把距离 {u , v}最近的点 w 加入到 T 中；继续这个过程，直到所有的点都在 T 中。

过程如下：

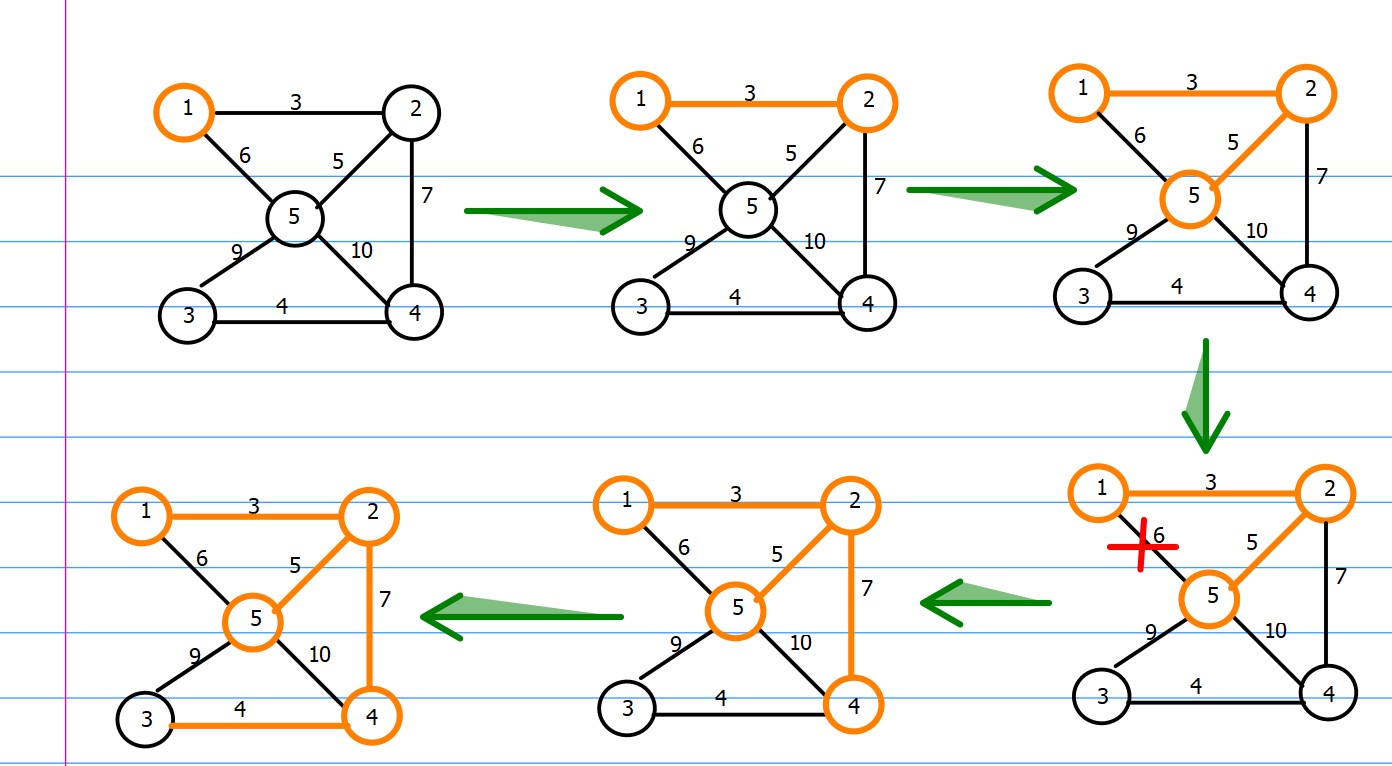
教科书代码如下

typedef struct
{
    int lowcost;
    int adjvex;
}Element;

void Prim(int arc[n][n],int w)
{
    int i,j,k;
    int Min;
    Element shortEdge[n];
    for(i=0;i < n;i++)// 初始化起点到其他的点的权值
    {
        shortEdge[i].lowcost=arc[w][i];
        shortEdge[i].adjvex=w;
    }
    shortEdge[w].lowcost=0;
    for(i=0;i < n-1;i++)
    {
        Min=100;
        for(j=0;j < n;j++)
        {
            if((shortEdge[j].lowcost!=0)&&(shortEdge[j].lowcost < Min))
            {
                Min=shortEdge[j].lowcost;
                k=j;
            }
        }
        cout<< shortEdge[k].adjvex<<"--"<< k<< endl;
        shortEdge[k].lowcost=0;
        for(j=0;j< n;j++)//更新数组
        {
            if(arc[k][j]< shortEdge[j].lowcost)
            {
                shortEdge[j].lowcost=arc[k][j];
                shortEdge[j].adjvex=k;
            }
        }
    }
}

模版代码

const int N = 510, INF = 0x3f3f3f3f;

int n, m;
int g[N][N];
int dist[N];
bool st[N];

int prim()
{
    memset(dist, 0x3f, sizeof dist);
    memset(st,false,sizeof st);
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            //!st[j]表示的是这个点没有被用过
            //(t == -1 || dist[t] > dist[j])
            //代表的是要么是第一次开始找（也就是t == -1)的情况
            //要么找到了一个点j，集合到点j的距离小于到t的距离，就更新t
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        if (i && dist[t] == INF) return INF;

        if (i) res += dist[t];
        st[t] = true;

        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
    }
    return res;
}

(kruskal)克鲁斯卡尔算法（边）

思想：对边进行贪心操作。从最短的边开始，把它加入到 T 中；在剩下的边中找最短的边，加入到 T 中；继续这个过程，直到所有边都在 T 中。

过程如下：

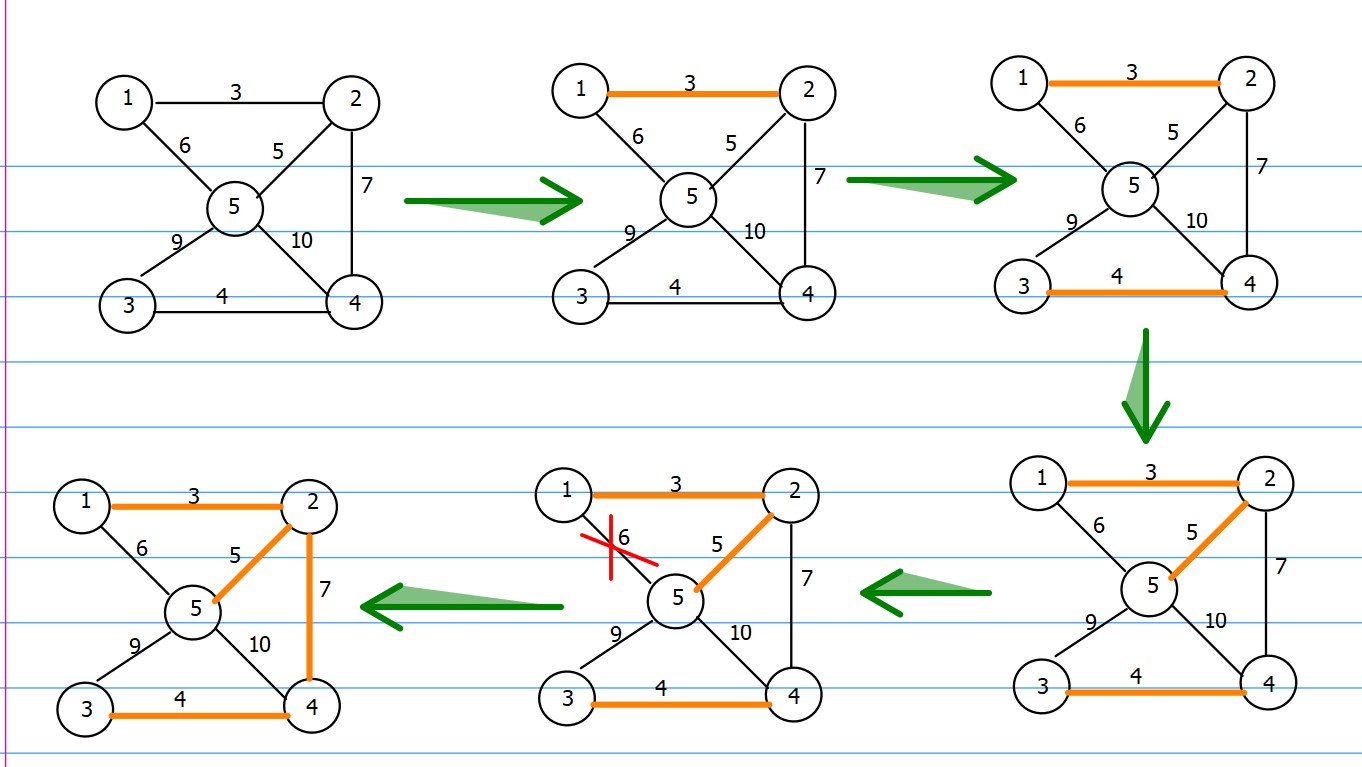
kruskal算法编程有以下两个关键技术

① 对边进行排序。可以用STL的sort()函数，排序后，依次把最短的边加入到 T 中。

② 判断圈，即处理连通性问题。这个问题用并查集简单而高效，并查集是kruskal算法的绝配。

kruskal + 并查集的代码如下(hdu 1233)：

const int NUM=103;
int S[NUM];//并查集
struct Edge{//定义边
    int u,v,w;
}edge[NUM*NUM];

bool cmp(Edge a,Edge b){return a.w<b.w;}

int find(int u){return S[u]==u?u:find(S[u]);}//查询并查集，返回u的根节点

int n,m;

int kruskal()
{
    int ans=0;
    for(int i=1;i<=n;i++)S[i]=i;//初始化，开始时每个点都是单独的集
    sort(edge+1,edge+1+m,cmp);
    for(int i=1;i<=m;i++)
    {
        int b=find(edge[i].u);//边的前端点u属于哪个集
        int c=find(edge[i].v);//边的后端点v属于哪个集
        if(b==c)continue;//产生圈，丢弃这个边
        S[c]=b;//合并
        ans+=edge[i].w;//计算MST
    }
    return ans;
}

附题：